Last Updated on February 12, 2024

Experimenting With the 3n+1 Sequence

Instructions

In this lab my job was to take the initial code, graph the iterations and find the max number of iterations from one of the 50 sequence starts. 

Initial Code

# Runestone.Academy thinkcspy course
# Chapter 8
# Lab

def seq3np1(n):
    """ Print the 3n+1 sequence from n, terminating when it reaches 1."""
    
    while n != 1:       
        print(n)
        if n % 2 == 0:        # n is even
            n = n // 2
        else:                 # n is odd
            n = n * 3 + 1
    print(n)                  # the last print is 1

My Code

# Runestone.Academy thinkcspy course
# Chapter 8
# Lab

import turtle

border = 10

def writeData(tt, itr, height):
    tt.goto(0-border, 0-border)
    tt.up()

    if height >= 100:
        tt.left(90)
        tt.forward(height+20)
        tt.right(90)
        tt.forward(itr*39)
        tt.write(str(height), move=False, align='center', font=('Times New Roman', 30, 'normal'))
        tt.forward(70)        
        tt.write(str(itr), move=False, align='center', font=('Times New Roman', 30, 'normal')) 
    else:                        # this is here so the last bar actually fills
        tt.left(90)
        tt.forward(height)
        tt.right(90)
        tt.forward(itr*40)
        tt.right(90)
        tt.forward(height)
        tt.left(90)
    
def drawBar(t, height):
    """ Get turtle t to draw one bar, of height. """
    t.begin_fill()               # start filling this shape
    t.left(90)
    t.forward(height)
    t.right(90)
    t.forward(40)
    t.right(90)
    t.forward(height)
    t.left(90)
    t.end_fill()                 # stop filling this shape

    
def seq3np1(n):
    """ Print the 3n+1 sequence from n, terminating when it reaches 1."""
    count = 1
    
    while n != 1:
        count += 1
       
        #print(n)
        if n % 2 == 0:        # n is even
            n = n // 2
        else:                 # n is odd
            n = n * 3 + 1
    #print(n)                 # the last print is 1
    #print(count)
    return count
    
    
wn = turtle.Screen()             # Set up the window and its attributes
wn.setworldcoordinates(0-border, 0-border, 40*50+border, 150)
wn.bgcolor("lightblue")
wn.tracer(100)

tess = turtle.Turtle()           # create tess and set some attributes
tess.color("purple")
tess.fillcolor("magenta")
tess.pensize(3)

alex = turtle.Turtle()
alex.color("purple")

maxSoFar = 0

for i in range(50):
    start = i + 1
    result = seq3np1(start)

    #print("Number of iterations to get to '1' from", start, ":", result)
    
    drawBar(tess, result)
    writeData(alex, start, result)
    
    if result > maxSoFar:
        maxSoFar = result

print("The max number of iterations was", maxSoFar, "from sequence start", start)

Result

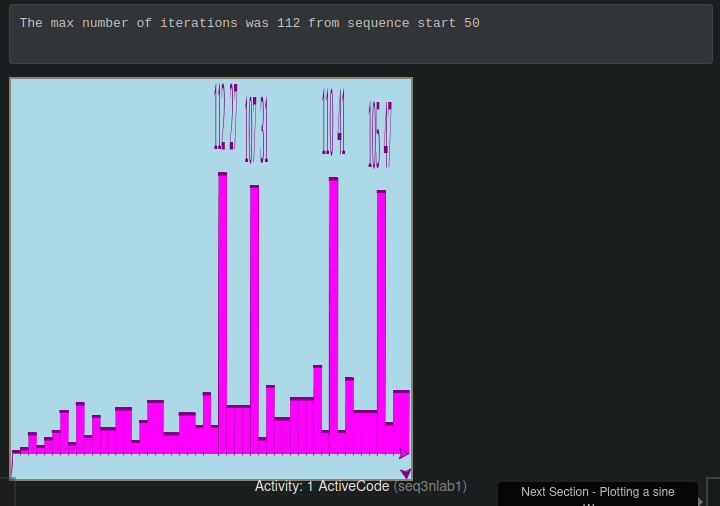
The numbers are not very readable, but it gets the job done.